MySQL にいい感じにコントリビュートする方法(非公式)
この記事は MySQLのカレンダー | Advent Calendar 2023 - Qiita 6 日目の記事です。
はじめに
どうも、この時期になるといつかのメリークリスマスを無限ループするけんつです。
世間の MySQLer を生業とする皆さん、唐突に MySQL をビルドしたくなったり急に徹夜でデバッグしたくなることが良くあると思いますが「なんだこれは」という挙動に遭遇することも稀によくあると思います。
例えば、何故かビルドがどこかのバージョンからすんなり通らなくなったり、どこかのバージョンから急にクソデカトランザクションの commit でハングったりといったやつです。
そんな時に気合いで原因を突き止め、これで直るんじゃないかというところまで辿り着き、更には修正方法までわかってしまったケースも稀によくあると思います。
今回はそんな気の触れた MySQLer に捧げる、カッとなって*1 パッチを書いてしまった場合のコントリビュートの方法についてです。
補足
流石にこの記事を書くためだけにまた Oracle のアカウントを作るのは面倒だったので、実際にパッチを出した時の記憶を思い出しながら書くのでところどころ正確さに欠ける場合があるかもしれないです。
コントリビュートしようぜ
登場人物
さほどいないですが、最初に登場人物を紹介します。
まずはみんな大好き MySQL Bugs です。バグ報告だったり、パッチを送りつける場合は基本的にこいつを経由します。
bugs.mysql.com
次は OSS にコントリビュートしたことのある人だと、CLA への署名を求められるという経験をしたことがある人もいるかと思います。それの Oracle 版の OCA というやつです。鬼門です。
oca.opensource.oracle.com
Oracle Profile の作成
登場人物を把握したところで MySQL Bugs からパッチを送りつけましょう、というだけですが Bug report/Contributionsを投げるためにまずは Oracle のアカウントが必要になります。
まずはこれを作らんことには何も始まらないので MySQL Bugs の右上にある register からアカウントを作成します。メールアドレスだったり、会社情報だったり諸々を入力して作成するだけです。
OCA への署名
Oracle Profile を作成したからといって勇み足でパッチを投げつける前に深呼吸をしてから OCA への署名を行います。OCA への署名がないと、パッチを受け取ってもらえない & OCA が Approve されるまでに担当者と何往復かコメントのやり取りが発生するので双方の手間を省くためにまずは署名からです。
OCA への署名は上のリンクから元気に作成していきます。種類は Company Agreement, Individual Agreement の二つがありますが、パッチの事情に応じて選択してください。*2
大体個人の時間で発掘したものしかやったことはないので、Individual Agreement への署名を前提にこのあとは語ります。
署名時に Oracle Profile の作成と同様の内容を書いたり・勝手に反映されたりするので必須情報のうち大半で苦労することはないと思います。
問題は Github account と Project です。github で管理されている mysql-server repository から、プルリクを投げる場合はこいつがかなり重要な役割を果たすそうです。果たすそうです、というのは Pull Request 経由でコントリビュートをやったことがないのですが、野生の有識者に聞くと OCA に署名した時に登録した github のアカウントから Pull Request が飛んでくると MySQL bugs にコピーして Pull Request を Close するという動きになるらしいということがわかりました。登録しておいて損はないはずなので、正しく入力しておきましょう。ただし、自分がやったことがないので Pull Request 経由は今回のスコープ外とします。
次に単純に罠な Project です。ここはコントリビュートしたいプロジェクトを選択して、プロジェクト単位で OCA への署名を行うようですが。単純にドロップダウンメニューを開いただけでは MySQL という文字列が見つからないです。しかし、検索ボックスに MySQL と入力すると関連プロジェクトが山のように出てくるという動きになっています。
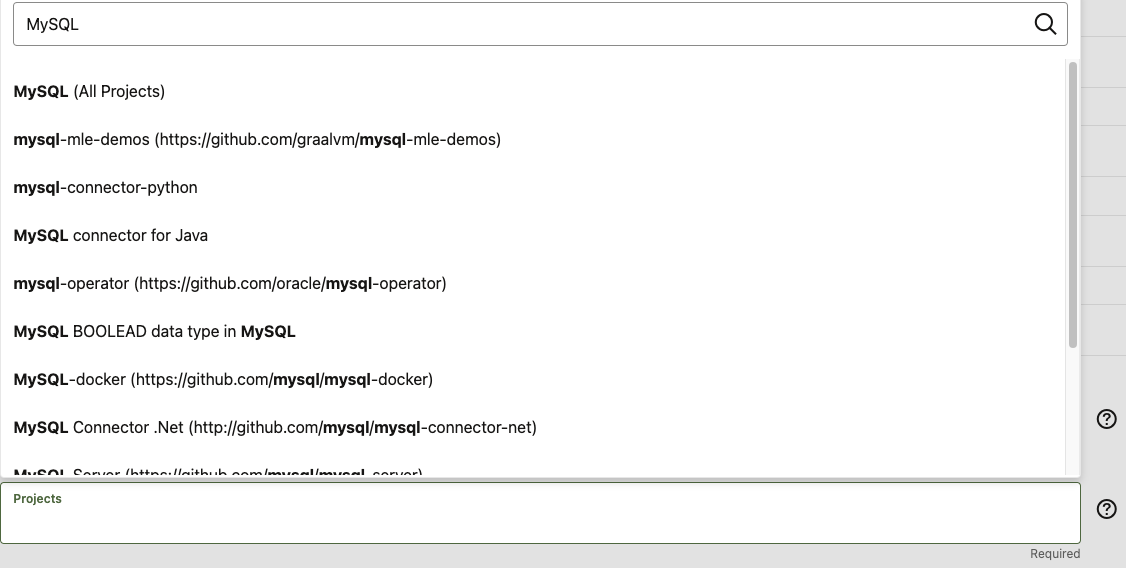
こんな感じです↑
MySQL 関連のプロジェクトで、コントリビュートしたプロジェクトだけを選択しても良いですし、自分だといつ何時 MySQL 関連のどのプロジェクトにコントリビュートするかわからないので All Projects にしています。
この罠をかわしたら、元気に次へと進めていくだけです。
ただし、最後の罠が待ち受けていて OCA の一覧から Approve されるのを待った方が良いです。署名はこの Approve をもって完了とするみたいです。*3

これです↑
魂のコントリビュート
ここまで怒涛の準備を超えていよいよ MySQL Bugs からコントリビュートです。
まずは MySQL Bugs の上のメニューにある Report a Bug を開き、起きている問題や再現方法、想定される解決策などを必要なものを埋めてまずは起票します。
残念な英語力ですが、自分が送ったパッチの時は以下のように書きました。
bugs.mysql.com
ここまできたら、起票したバグの Contribute タブから patch ファイルを添付してあげます。これは patch コマンドの出力結果か、良いかわからないですが git diff の出力でも受け取ってもらえたのでどちらかでやるのが無難だと思います。
そうすると担当者からコメントがやってくるので、必要に応じてやり取りをしながら気長に行末を見守ってコントリビュートは完了です。
追記 2023/12/06 19:34
このブログを投稿した後に yoku さんから情報がやってきた。どうやら Pull Request 経由のバグレポを発掘したと。
ちなみにgithubから転記されたhttps://t.co/CNL96SPQ8Aはこんな感じです。https://t.co/r1kNS6MJuC
— yoku0825 (@yoku0825) 2023年12月6日
github側はこんなhttps://t.co/apBImSc7XJ
— yoku0825 (@yoku0825) 2023年12月6日
MySQL Bugs: #102405: Contribution: openssl v3 support
openssl v3 support by macvk · Pull Request #320 · mysql/mysql-server · GitHub
これらの様子を見ていると、Pull Request の Description と Diff がそのまま MySQL Bugs の Description と Contributions に反映されて Close されている。
差分がでかくなったらこれのほうが楽なのでよい情報をもらった。
無事に取り込まれると…
git log に名前が残る
よくあるやつです。嬉しい。
❯ git log --grep="35442825"
commit 385ccdd4e1c53eadfdeed9080a80c8fa8162808c
Author: Tor Didriksen <tor.didriksen@oracle.com>
Date: Tue May 30 15:42:51 2023 +0200
Bug#35442825 Build fails with LANG=ja_JP.UTF-8
Set LANG=C in the environment when executing readelf, to avoid any
problems with non-ascii output.
Patch is based on a contribution from Kento Takeuchi.
Change-Id: I2a7e4dead3208aa5bb65f7d86b766e76fbb7b9c5
(cherry picked from commit 37a5f2c7a195d021186e40eef9738646e87ead74)
ブログで紹介してもらえる
粋な計らいです。*4 とっても嬉しい。
MySQL 8.1.0 is out ! Thank you for the contributions !!
https://blogs.oracle.com/mysql/post/mysql-810-is-out-thank-you-for-the-contributions
This new Innovation Release already contains contributions from our great Community. MySQL 8.1.0 contains patches from Meta (Facebook), Allen Long, Daniël van Eeden, Brent Gardner, Yura Sorokin (Percona) and Kento Takeuchi.
...
#111190 – Build fails with LANG=ja_JP.UTF-8 – Kento Takeuchi
Handler と SELECT と時々 WHERE 句
はじめに
どうも、最近どうにか出費を抑えようとしているけんつです。今回は自作ストレージエンジンをやっていて気になった SELECT と WHERE が組み合わさったときの挙動について書こうかなと思います。自作ストレージエンジンを前提にしているので、InnoDB などはこの限りではない可能性が十分にあります。
環境
- MySQL 8.0.33
- PopOS 22.04
- 自作ストレージエンジン
前提
また例によって mtr を使ってクエリを実行しながらデバッグする。mtr に食わせる test, result ファイルは以下の通り。やっていることは単純で2つレコードを追加して、条件にマッチするレコードが1つ返ってくるというもの。
CREATE TABLE t1(id INT)Engine=Toybox; INSERT INTO t1(id) VALUES(1); INSERT INTO t1(id) VALUES(2); SELECT * FROM t1 WHERE id > 1; DROP TABLE t1;
CREATE TABLE t1(id INT)Engine=Toybox; INSERT INTO t1(id) VALUES(1); INSERT INTO t1(id) VALUES(2); SELECT * FROM t1 WHERE id > 1; id 2 DROP TABLE t1;
このテストを実行すると無事に PASS するので元気にデバッグする。toybox というのは今作っている自作ストレージエンジンの名前です。
$ ./mtr toybox.select_where
Logging: /home/lrf141/mysqlProject/mysql-server/mysql-test/mysql-test-run.pl toybox.select_where
MySQL Version 8.0.33
Checking supported features
- Binaries are debug compiled
Using 'all' suites
Collecting tests
Checking leftover processes
- found old pid 30513 in 'mysqld.1.pid', killing it...
ok!
Removing old var directory
Creating var directory '/home/lrf141/mysqlProject/mysql-server/build/mysql-test/var'
Installing system database
Using parallel: 1
==============================================================================
TEST NAME RESULT TIME (ms) COMMENT
------------------------------------------------------------------------------
[ 50%] toybox.select_where [ pass ] 21
[100%] shutdown_report [ pass ]
------------------------------------------------------------------------------
The servers were restarted 0 times
The servers were reinitialized 0 times
Spent 0.021 of 25 seconds executing testcases
Completed: All 2 tests were successful.
さぁデバッグタイムだ
後は元気にデバッグしていくだけなので読む。
確実に発生している事実
まずは何がどうなっているか事実を確認する。
現段階の実装では rnd_next という(おそらく)テーブルスキャンで各行を読み出すメソッドを通過する。これが一体何回通過するのかというのが重要な事柄となる。
(rr) c Continuing. Thread 2 hit Breakpoint 1, ha_toybox::rnd_next (this=0x7f9750482300, buf=0x7f9750464e70 "\377") at /home/lrf141/mysqlProject/mysql-server/storage/toybox/ha_toybox.cc:553 warning: Source file is more recent than executable. 553 filesort.cc, records.cc, sql_handler.cc, sql_select.cc, sql_table.cc and (rr) c Continuing. Thread 2 hit Breakpoint 1, ha_toybox::rnd_next (this=0x7f9750482300, buf=0x7f9750464e70 "") at /home/lrf141/mysqlProject/mysql-server/storage/toybox/ha_toybox.cc:553 553 filesort.cc, records.cc, sql_handler.cc, sql_select.cc, sql_table.cc and (rr) c Continuing. Thread 2 hit Breakpoint 1, ha_toybox::rnd_next (this=0x7f9750482300, buf=0x7f9750464e70 "") at /home/lrf141/mysqlProject/mysql-server/storage/toybox/ha_toybox.cc:553 553 filesort.cc, records.cc, sql_handler.cc, sql_select.cc, sql_table.cc and (rr) c Continuing.
通過するのは 3 回となった。これが INSERT した 2 回ではないのは rnd_next の終了条件として HA_ERR_END_OF_FILE を返す必要があるからである。詳しくは以下の記事で紹介している。
rabbitfoot141.hatenablog.com
これによってテーブルスキャンの場合に限り WHERE 句で指定された条件によって handler が一致するレコードを取得するわけではなく、全てのレコードを返しているということがわかる。
ちなみにそのときの backtrace は以下の通り。
(rr) bt
#0 ha_toybox::rnd_next (this=0x7f9750482300, buf=0x7f9750464e70 "")
at /home/lrf141/mysqlProject/mysql-server/storage/toybox/ha_toybox.cc:553
#1 0x0000555ae12d5992 in handler::ha_rnd_next (this=0x7f9750482300, buf=0x7f9750464e70 "")
at /home/lrf141/mysqlProject/mysql-server/sql/handler.cc:2970
#2 0x0000555ae14b000a in TableScanIterator::Read (this=0x7f97504868f8)
at /home/lrf141/mysqlProject/mysql-server/sql/iterators/basic_row_iterators.cc:219
#3 0x0000555ae16fe8c3 in FilterIterator::Read (this=0x7f9750486940)
at /home/lrf141/mysqlProject/mysql-server/sql/iterators/composite_iterators.cc:76
#4 0x0000555ae1009aeb in Query_expression::ExecuteIteratorQuery (this=0x7f975039ee00,
thd=0x7f97506bc4a0) at /home/lrf141/mysqlProject/mysql-server/sql/sql_union.cc:1770
#5 0x0000555ae1009e87 in Query_expression::execute (this=0x7f975039ee00, thd=0x7f97506bc4a0)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_union.cc:1823
#6 0x0000555ae0f49104 in Sql_cmd_dml::execute_inner (this=0x7f97504851c8,
thd=0x7f97506bc4a0) at /home/lrf141/mysqlProject/mysql-server/sql/sql_select.cc:799
#7 0x0000555ae0f484f5 in Sql_cmd_dml::execute (this=0x7f97504851c8, thd=0x7f97506bc4a0)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_select.cc:578
#8 0x0000555ae0ebb4d4 in mysql_execute_command (thd=0x7f97506bc4a0, first_level=true)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:4714
#9 0x0000555ae0ebd91d in dispatch_sql_command (thd=0x7f97506bc4a0,
parser_state=0x7f972c5e69f0)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:5363
#10 0x0000555ae0eb2da3 in dispatch_command (thd=0x7f97506bc4a0, com_data=0x7f972c5e7340,
command=COM_QUERY) at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:2050
#11 0x0000555ae0eb0c0d in do_command (thd=0x7f97506bc4a0)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:1439
#12 0x0000555ae10fd937 in handle_connection (arg=0x555ae8b3d910)
at /home/lrf141/mysqlProject/mysql-server/sql/conn_handler/connection_handler_per_thread.cc:302
#13 0x0000555ae33989fe in pfs_spawn_thread (arg=0x555ae9f44d30)
at /home/lrf141/mysqlProject/mysql-server/storage/perfschema/pfs.cc:3042
#14 0x00007f976b694ac3 in start_thread (arg=<optimized out>) at ./nptl/pthread_create.c:442
#15 0x00007f976b725bf4 in clone () at ../sysdeps/unix/sysv/linux/x86_64/clone.S:100FilterIterator::Read, Query_expression::ExecuteIteratorQuery とか大変それっぽいやつを通過しているのでそのあたりをこれから見ている。
いざ server レイヤーダイブ
流石に Query Executor はコードパスのうち、どこを見ていけばいいのかわからないので今回も元気に先頭から読んでいくという筋力プレイに走る。
最初は TableScanIterator::Read から読む。
while ((tmp = table()->file->ha_rnd_next(m_record))) { /* ha_rnd_next can return RECORD_DELETED for MyISAM when one thread is reading and another deleting without locks. */ if (tmp == HA_ERR_RECORD_DELETED && !thd()->killed) continue; return HandleError(tmp); } if (m_examined_rows != nullptr) { ++*m_examined_rows; }
まずこの部分で handler の rnd_next を行ってテーブルから一行読み出す。これは前述のブログ記事に詳細を書いているので解説は省く。
次にたどり着くのは FilterIterator::Read の以下の実装となる。
int err = m_source->Read(); if (err != 0) return err; bool matched = m_condition->val_int(); if (thd()->killed) { thd()->send_kill_message(); return 1; } /* check for errors evaluating the condition */ if (thd()->is_error()) return 1; if (!matched) { m_source->UnlockRow(); continue; } // Successful row. return 0;
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/iterators/composite_iterators.cc#L76-L95
ここで大変重要になってくるのは、 m_condition->val_int() である。
何故かというと一行目と二行目で今回のテストケースでは二行目のみが結果としてクライアントに返却されるが、この戻り値の bool が各行の読み出しで結果が異なるためである。
# 一行目の呼び出しと matched の値
(rr) c
Continuing.
Thread 41 hit Breakpoint 4, TableScanIterator::Read (this=0x7f97504868f8) at /home/lrf141/mysqlProject/mysql-server/sql/iterators/basic_row_iterators.cc:219
219 while ((tmp = table()->file->ha_rnd_next(m_record))) {
(rr) c
Continuing.
Thread 41 hit Breakpoint 1, ha_toybox::rnd_next (this=0x7f9750482300, buf=0x7f9750464e70 "\377") at /home/lrf141/mysqlProject/mysql-server/storage/toybox/ha_toybox.cc:553
warning: Source file is more recent than executable.
553 filesort.cc, records.cc, sql_handler.cc, sql_select.cc, sql_table.cc and
(rr) c
Continuing.
Thread 41 hit Breakpoint 3, FilterIterator::Read (this=0x7f9750486940) at /home/lrf141/mysqlProject/mysql-server/sql/iterators/composite_iterators.cc:81
81 if (thd()->killed) {
(rr) p matched
$15 = false
# 二行目の呼び出しと matched の値
(rr) c
Continuing.
Thread 41 hit Breakpoint 4, TableScanIterator::Read (this=0x7f97504868f8) at /home/lrf141/mysqlProject/mysql-server/sql/iterators/basic_row_iterators.cc:219
219 while ((tmp = table()->file->ha_rnd_next(m_record))) {
(rr) c
Continuing.
Thread 41 hit Breakpoint 1, ha_toybox::rnd_next (this=0x7f9750482300, buf=0x7f9750464e70 "") at /home/lrf141/mysqlProject/mysql-server/storage/toybox/ha_toybox.cc:553
553 filesort.cc, records.cc, sql_handler.cc, sql_select.cc, sql_table.cc and
(rr) c
Continuing.
Thread 41 hit Breakpoint 3, FilterIterator::Read (this=0x7f9750486940) at /home/lrf141/mysqlProject/mysql-server/sql/iterators/composite_iterators.cc:81
81 if (thd()->killed) {
(rr) p matched
$16 = true確かに一行目と二行目で matched の値がそれぞれ false, true になっている。matched が false になると continue に入り、次の行を読み出すようにする。
そしてその処理が何に影響を与えるかというと、Query_expression::ExecuteIteratorQuery にある以下の実装を呼び出すかどうかに影響を与える。
for (;;) { int error = m_root_iterator->Read(); DBUG_EXECUTE_IF("bug13822652_1", thd->killed = THD::KILL_QUERY;); if (error > 0 || thd->is_error()) // Fatal error return true; else if (error < 0) break; else if (thd->killed) // Aborted by user { thd->send_kill_message(); return true; } ++*send_records_ptr; if (query_result->send_data(thd, *fields)) { return true; } thd->get_stmt_da()->inc_current_row_for_condition(); }
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_union.cc#L1769-L1789
この段階では m_root_iterator->Read() は rnd_next の戻り値となる 0 を引っ張ってくるので、 query_result->send_data の呼び出しに到達する。
まとめ
というわけでテーブルスキャンを伴う SELECT と WHERE 句の扱いは以下のようになっている。
- handler はテーブルに含まれる全ての行を読み出す
- server layer でそれが条件に合うかどうかを判定する
- 条件に一致する場合はレコードの情報をクライアントに返却する
おわりに
結構雑にはなったが、大まかな処理としてテーブルスキャンが伴う WHERE 句の動きについて理解することができた。
今回知り得た情報以上の内容を知りたくなった場合は条件をどのように構造体として表現しているか、Iterator の選択はどのように行っているかを見ていく必要がありそうだが、今回はここまでとする。
テーブルスキャン時に呼ばれる rnd_next については分かってきたが、これと似たようなインターフェースを持つものに UPDATE, DELETE が存在するのでその場合の WHERE 句はどのように制御されるのかをまた今度調べてみようと思う。
LOAD DATA LOCAL INFILE ~ REPLACE INTO と時々ロックでしっかり沼った
はじめに
どうも、最近よく主要人物が闇落ちする映像作品を薦められがちなけんつです。最近色々あって LOAD DATA LOCAL INFILE ~ REPLACE INTO ~ を呼んだときにどういった処理が走るのか、特に metadata lock 周りが気になったのでそれについて書きます。大層ご立派なことを書いているが、完全にメモである。ブログ書きながら読める分量じゃなかった。
そして余談だが、どこで何のロックがかかっているのかを知りたい時が最近多すぎる。
書きながら思ったこと
本当は InnoDB まで見ようと思ったが思いの外手強かったので metadata lock 周りが中心になりそう。むしろ metadata lock も全部読めているか怪しい。
検証する
前提
LOAD DATA INFILE を実行した場合に通過するコードパスがわからなかったので、以下の test, result ファイルを用意して mtr を実行し debug trace を取得する。
create table t1(id int)Engine=InnoDB; insert into t1(id) values(1),(2),(3),(4); load data infile '../../std_data/hoge.csv' replace into table t1 fields terminated by ','; drop table t1;
create table t1(id int)Engine=InnoDB; insert into t1(id) values(1),(2),(3),(4); load data infile '../../std_data/hoge.csv' replace into table t1 fields terminated by ','; drop table t1;
また std_data 以下に適当な名前の csv ファイルを追加し、以下の内容とする。
1 2 3
コードパスを掴む
コードパスがわからないとどこを見れば良いかわからないので debug trace, gdb とにらめっこしながらどこを通過するのか、ということからまず調べる必要がある。
debug trace を見ていると以下のような処理がいくつか流れていることがわかる。
... T@11: | | | | >Sql_cmd_load_table::execute_inner T@11: | | | | | >THD::set_current_stmt_binlog_format_row_if_mixed T@11: | | | | | <THD::set_current_stmt_binlog_format_row_if_mixed T@11: | | | | | >open_and_lock_tables T@11: | | | | | | >open_tables T@11: | | | | | | | THD::enter_stage: 'Opening tables' /home/lrf141/mysqlProject/mysql-server/sql/sql_base.cc:5795 T@11: | | | | | | | >PROFILING::status_change T@11: | | | | | | | <PROFILING::status_change T@11: | | | | | | | >open_and_process_table T@11: | | | | | | | | >debug_sync T@11: | | | | | | | | | debug_sync_point: hit: 'open_and_process_table' T@11: | | | | | | | | <debug_sync T@11: | | | | | | | | tcache: opening table: 'test'.'file_tbl' item: 0x7f3d4c29f008 T@11: | | | | | | | | >ha_innobase::update_thd T@11: | | | | | | | | | ha_innobase::update_thd: user_thd: 0x7f3d4c5a9a30 -> 0x7f3d4c5a9a30 T@11: | | | | | | | | | >innobase_trx_init T@11: | | | | | | | | | <innobase_trx_init T@11: | | | | | | | | <ha_innobase::update_thd T@11: | | | | | | | <open_and_process_table T@11: | | | | | | | >debug_sync T@11: | | | | | | | | debug_sync_point: hit: 'open_tables_after_open_and_process_table' T@11: | | | | | | | <debug_sync T@11: | | | | | | | open_tables: returning: 0 T@11: | | | | | | <open_tables T@11: | | | | | | >lock_tables ...
コードパスはわからないとしても write_row は通過するはずと、ha_innobase::write_row にブレークポイントを貼って更に実行する。
すると以下の back trace となる。
(gdb) bt
#0 ha_innobase::write_row (this=0x7fff3c125620, record=0x7fff3c00f1f0 "\375\001")
at /home/lrf141/mysqlProject/mysql-server/storage/innobase/handler/ha_innodb.cc:8972
#1 0x000055555917c6f2 in handler::ha_write_row (this=0x7fff3c125620,
buf=0x7fff3c00f1f0 "\375\001")
at /home/lrf141/mysqlProject/mysql-server/sql/handler.cc:7953
#2 0x0000555559529e78 in write_record (thd=0x7fff3c001050, table=0x7fff3c0f54d0,
info=0x7fffd85f2ef0, update=0x0)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_insert.cc:1811
#3 0x0000555559534cc4 in Sql_cmd_load_table::read_sep_field (this=0x7fff3c11ed28,
thd=0x7fff3c001050, info=..., table_list=0x7fff3c11ee60, read_info=..., enclosed=...,
skip_lines=0) at /home/lrf141/mysqlProject/mysql-server/sql/sql_load.cc:1109
#4 0x0000555559532d19 in Sql_cmd_load_table::execute_inner (this=0x7fff3c11ed28,
thd=0x7fff3c001050, handle_duplicates=DUP_REPLACE)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_load.cc:570
#5 0x00005555595390df in Sql_cmd_load_table::execute (this=0x7fff3c11ed28,
thd=0x7fff3c001050) at /home/lrf141/mysqlProject/mysql-server/sql/sql_load.cc:2147
#6 0x0000555558d4edfb in mysql_execute_command (thd=0x7fff3c001050, first_level=true)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:3683
#7 0x0000555558d5491d in dispatch_sql_command (thd=0x7fff3c001050,
parser_state=0x7fffd85f49f0)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:5363
#8 0x0000555558d49da3 in dispatch_command (thd=0x7fff3c001050, com_data=0x7fffd85f5340,
command=COM_QUERY) at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:2050
#9 0x0000555558d47c0d in do_command (thd=0x7fff3c001050)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:1439
#10 0x0000555558f94937 in handle_connection (arg=0x55556093e800)
at /home/lrf141/mysqlProject/mysql-server/sql/conn_handler/connection_handler_per_thread.cc:302
#11 0x000055555b22f9fe in pfs_spawn_thread (arg=0x555560dde4b0)
at /home/lrf141/mysqlProject/mysql-server/storage/perfschema/pfs.cc:3042
#12 0x00007ffff7294ac3 in start_thread (arg=<optimized out>) at ./nptl/pthread_create.c:442
#13 0x00007ffff7326a40 in clone3 () at ../sysdeps/unix/sysv/linux/x86_64/clone3.S:81Sql_cmd_load_table::execute_inner から先はメソッド名を見るに、各 field を読み込みながらストレージエンジンの write_row を呼び出すという流れになっていると読み取れる。
次に、念の為 ha_innobase::write_row を通過するときに引数として渡ってくるバイナリ列を見る。
(gdb) b ha_innobase::write_row
Breakpoint 3 at 0x55555a614e14: file /home/lrf141/mysqlProject/mysql-server/storage/innobase/handler/ha_innodb.cc, line 8972.
(gdb) c
Continuing.
InnoDB: ###### Diagnostic info printed to the standard error stream
Thread 48 "connection" hit Breakpoint 3, ha_innobase::write_row (this=0x7fff3c125620, record=0x7fff3c00f1f0 "\375\001") at /home/lrf141/mysqlProject/mysql-server/storage/innobase/handler/ha_innodb.cc:8972
8972 {
// 一回目の write_row
(gdb) p *(record)
$9 = 253 '\375'
(gdb) p *(record + 1)
$10 = 1 '\001'
// 二回目の write_row
(gdb) p *(record + 0)
$12 = 253 '\375'
(gdb) p *(record + 1)
$13 = 2 '\002'
// 三回目の write_row
(gdb) p *(record + 0)
$14 = 253 '\375'
(gdb) p *(record + 1)
$15 = 3 '\003'handler::write_row の引数で渡ってくるバイト列は Row Format になっていて、この場合先頭 1 byte は null bitmap で次の 4 byte が test, result ファイルで宣言した INT カラムの値となっている。
また、ここで四回止まるなら最初に 1~4 を INSERT している部分であるが、三回しか止まらないので前もって用意した csv ファイルの中身が insert される瞬間であるということがわかる。
というわけで Sql_cmd_load_table::execute_inner から先を読んでいけば良いということがわかった。
ちょっと気合を入れて読んでいく
というわけでこのあたりから元気に読んでいく。
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_load.cc#L192-L201
まず最初に気になるのはここ。
/* Bug #34283 mysqlbinlog leaves tmpfile after termination if binlog contains load data infile, so in mixed mode we go to row-based for avoiding the problem. */ thd->set_current_stmt_binlog_format_row_if_mixed();
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_load.cc#L226-L232
これの中身を追っていくと、ここにたどり着く
if ((variables.binlog_format == BINLOG_FORMAT_MIXED) && (in_sub_stmt == 0)) set_current_stmt_binlog_format_row();
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_class.h#L3396-L3397
inline void set_current_stmt_binlog_format_row() { DBUG_TRACE; current_stmt_binlog_format = BINLOG_FORMAT_ROW; return; }
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_class.h#L3401-L3405
binlog_format が MIXED になっている場合で、trigger か stored function の場合は ROW を設定している。
これは
MySQL Bugs: #34283: mysqlbinlog leaves tmpfile after termination if binlog contains load data infile
このバグが関連していて、mysqlbinlog が生成する tmp ファイルが残らないようにするための措置っぽい雰囲気を感じる。が、今はこれは主題ではないのでこのぐらいにする。2008 年頃からずっとあるみたいだし。
これの後は LOAD DATA INFILE で与えられているセパレータなどの文字列が ascii かどうかを確認しているが、これも今回見たいことではないので一旦飛ばす。
もし具体的にどんな値が渡されているかをみたい時は is_ascii() が呼び出されている各変数の m_ptr を参照すれば見ることができる。
次はいよいよ面白くなってきて lock 周りに突入するこの部分。
if (open_and_lock_tables(thd, table_list, 0)) return true;
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_load.cc#L248
これを追っていくと、以下の関数にたどり着く。ここではテーブルを開いてロックをかけるという流れになっているので、それぞれ見ていく。
/** Open all tables in list, locks them and optionally process derived tables. @param thd Thread context. @param tables List of tables for open and locking. @param flags Bitmap of options to be used to open and lock tables (see open_tables() and mysql_lock_tables() for details). @param prelocking_strategy Strategy which specifies how prelocking algorithm should work for this statement. @note The thr_lock locks will automatically be freed by close_thread_tables(). @note open_and_lock_tables() is not intended for open-and-locking system tables in those cases when execution of statement has started already and other tables have been opened. Use open_trans_system_tables_for_read() instead. @retval false OK. @retval true Error */ bool open_and_lock_tables(THD *thd, Table_ref *tables, uint flags, Prelocking_strategy *prelocking_strategy) {
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_base.cc#L6542-L6565
この関数をざっと読んでいくと open_table, lock_table という実にそれらしい関数を呼び出しているので、その2つを重点的に読んでいく。
まずは open_table から。
open_table に関する実装をデバッグしながら読んでいくと、まずは以下の実装にたどり着く。
Table_ref *table;
if (lock_table_names(thd, *start, thd->lex->first_not_own_table(),
ot_ctx.get_timeout(), flags)) {
error = true;
goto err;
}
for (table = *start; table && table != thd->lex->first_not_own_table();
table = table->next_global) {
if (table->mdl_request.is_ddl_or_lock_tables_lock_request() ||
table->open_strategy == Table_ref::OPEN_FOR_CREATE)
table->mdl_request.ticket = nullptr;
}
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_base.cc#L5825-L5836
なんとなく metadata lock に関するであろう処理がいくつかあるが、ここで重要になるのは lock_table_names。
何故かというと lock_table_names を読んでいると LOCK TABLES か DDL によって発生する metadata lock を取得するとあるため。
/** Acquire "strong" (SRO, SNW, SNRW) metadata locks on tables used by LOCK TABLES or by a DDL statement. Acquire lock "S" on table being created in CREATE TABLE statement. @note Under LOCK TABLES, we can't take new locks, so use open_tables_check_upgradable_mdl() instead. @param thd Thread context. @param tables_start Start of list of tables on which locks should be acquired. @param tables_end End of list of tables. @param lock_wait_timeout Seconds to wait before timeout. @param flags Bitmap of flags to modify how the tables will be open, see open_table() description for details. @param schema_reqs When non-nullptr, pointer to array in which pointers to MDL requests for acquired schema locks to be stored. It is guaranteed that each schema will be present in this array only once. @retval false Success. @retval true Failure (e.g. connection was killed) */ bool lock_table_names(THD *thd, Table_ref *tables_start, Table_ref *tables_end,
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_base.cc#L5357-L5382
ここのコメントはとてもよく書かれていて、以下の手順でロックを取得する
- 対象テーブルの一意な Schema Set を作成する
- Schema Set に対して Insert Intention Lock を設定する
- ここまでに設定したロックを取得する
- tablespace 名をロックする
最初の手順は良いとしても、その後にやってくる3つの手順に関しては実装を読みながらでないと自分で書いていても何を言っているかわからなくなる。
ざっくりとまとめるなら 2, 3 はある意味ではひとまとまりになっていて、2 が IX を各オブジェクトに設定し、3 で実際にロックを取得するという流れになっている。
そして最もよくわからなかった 4 についてだが、これは tablespace 名をロックしたいがそれには data dictionary を参照する必要があり、data dictionary を参照するには schema の metadata lock が必要になる、という事情があるらしい。
/* Phase 4: Lock tablespace names. This cannot be done as part of the previous phases, because we need to read the dictionary to get hold of the tablespace name, and in order to do this, we must have acquired a lock on the table. */ return get_and_lock_tablespace_names(thd, tables_start, tables_end, lock_wait_timeout, flags);
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_base.cc#L5506-L5512
この部分はこの程度で終わらせてしまっても良いが延々とコメントを引用しただけになってしまうので、忘れないために metadata lock を実装ではどうやって取得するかに少しだけ言及する。
まずここまでに挙げた実装を眺めると、やたら MDL_ という文字列を見かけるがこれは大体 metadata lock に関する情報を扱うデータ構造だったりする。
そして特に自分が理解するのに必要だったのは Phase 2 で、特に以下の部分。
for (const Table_ref *table_l : schema_set) { MDL_request *schema_request = new (thd->mem_root) MDL_request; if (schema_request == nullptr) return true; MDL_REQUEST_INIT(schema_request, MDL_key::SCHEMA, table_l->db, "", MDL_INTENTION_EXCLUSIVE, MDL_TRANSACTION); mdl_requests.push_front(schema_request); if (schema_reqs) schema_reqs->push_back(schema_request); }
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/sql/sql_base.cc#L5454-L5465
mdl_requests というのは要求したい metadata lock のリストとなっている。ここに突っ込んだ情報を元に Phase 3 で metadata lock が取得される。
そして次に面白かったのが MDL_REQUEST_INIT という謎マクロ。特にその引数は面白かった。
何が面白いかというと、MDL_INTENTION_EXCLUSIVE が IX を示していて、MDL_TRANSACTION が設定されているのでトランザクションの終了と共に自動で metadata lock が開放されるという風になっていること。思ったよりロックの寿命が長かった。だいぶ長かった。
というわけでこの後はいつものテーブルを元気に開くやつがやってくる。ここでも metadata lock 周りでなんかやっている雰囲気はあるが、一旦放置で。
信じられないことにここまでが open_table の内容である…。
この後は open_table と対になっている lock_table がやってくる。ここを読み切る気力はもうすでに失われたので、将来の自分のために backtrace だけ貼っておく。
読み切る気力がなくなったのは metadata lock の読解でもうだいぶカロリーを使った上に lock_table がやっているのは ha_innobase::external_lock を呼び出すことなので次回に持ち越し。どのみち自作ストレージエンジンのために一度は読む必要があるので。
(rr) bt
#0 ha_innobase::external_lock (this=0x7fc0b04587c0, thd=0x7fc0b0025f70, lock_type=1)
at /home/lrf141/mysqlProject/mysql-server/storage/innobase/handler/ha_innodb.cc:18583
#1 0x000055f86b1e815a in handler::ha_external_lock (this=0x7fc0b04587c0,
thd=0x7fc0b0025f70, lock_type=1)
at /home/lrf141/mysqlProject/mysql-server/sql/handler.cc:7884
#2 0x000055f86b46a167 in lock_external (thd=0x7fc0b0025f70, tables=0x7fc0b04545d8, count=1)
at /home/lrf141/mysqlProject/mysql-server/sql/lock.cc:393
#3 0x000055f86b469de5 in mysql_lock_tables (thd=0x7fc0b0025f70, tables=0x7fc0b06f6290,
count=1, flags=0) at /home/lrf141/mysqlProject/mysql-server/sql/lock.cc:337
#4 0x000055f86ac975a4 in lock_tables (thd=0x7fc0b0025f70, tables=0x7fc0b06f5830, count=1,
flags=0) at /home/lrf141/mysqlProject/mysql-server/sql/sql_base.cc:6899
#5 0x000055f86ac96b84 in open_and_lock_tables (thd=0x7fc0b0025f70, tables=0x7fc0b06f5830,
flags=0, prelocking_strategy=0x7fc089be6d60)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_base.cc:6593
#6 0x000055f86abec248 in open_and_lock_tables (thd=0x7fc0b0025f70, tables=0x7fc0b06f5830,
flags=0) at /home/lrf141/mysqlProject/mysql-server/sql/sql_base.h:470
#7 0x000055f86b59d818 in Sql_cmd_load_table::execute_inner (this=0x7fc0b06f56f8,
thd=0x7fc0b0025f70, handle_duplicates=DUP_REPLACE)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_load.cc:248
#8 0x000055f86b5a50df in Sql_cmd_load_table::execute (this=0x7fc0b06f56f8,
thd=0x7fc0b0025f70) at /home/lrf141/mysqlProject/mysql-server/sql/sql_load.cc:2147
#9 0x000055f86adbadfb in mysql_execute_command (thd=0x7fc0b0025f70, first_level=true)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:3683
#10 0x000055f86adc091d in dispatch_sql_command (thd=0x7fc0b0025f70,
parser_state=0x7fc089be89f0)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:5363
#11 0x000055f86adb5da3 in dispatch_command (thd=0x7fc0b0025f70, com_data=0x7fc089be9340,
command=COM_QUERY) at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:2050
#12 0x000055f86adb3c0d in do_command (thd=0x7fc0b0025f70)
at /home/lrf141/mysqlProject/mysql-server/sql/sql_parse.cc:1439
#13 0x000055f86b000937 in handle_connection (arg=0x55f87418e1b0)
at /home/lrf141/mysqlProject/mysql-server/sql/conn_handler/connection_handler_per_thread.cc:302
#14 0x000055f86d29b9fe in pfs_spawn_thread (arg=0x55f874192080)
at /home/lrf141/mysqlProject/mysql-server/storage/perfschema/pfs.cc:3042
#15 0x00007fc0c8c94ac3 in start_thread (arg=<optimized out>) at ./nptl/pthread_create.c:442
#16 0x00007fc0c8d25bf4 in clone () at ../sysdeps/unix/sysv/linux/x86_64/clone.S:100
おわりに
というわけでハイパー駆け足になったが metadata lock を中心に理解が深まった部分がいくつかある。特に metadata lock がどういう処理で取得されているか、取得までに必要な諸々のデータ構造についてわかったのはでかい。
そしてまだちゃんとデバッグしたわけではないが LOAD DATA LOCAL INFILE ~ REPLACE INTO は普通に data_locks を眺めていると
という風になっている。はず。
というわけで次回作にご期待ください。
MySQL 探索記 ~ Unit Test がビルドされる時に必要なライブラリとリンク~
はじめに
どうも、ユニットテストをかけるようになったぜと前回の記事で喜んでいたらバイナリの書き込みで盛大に 1byte ずれていることに気がついてしまったけんつです。
rabbitfoot141.hatenablog.com
最近、MySQL ごとビルドする場合に unittest/ 以外のディレクトリでユニットテストをサポートする方法について書いたが、いざ自分が作っているプラグインをビルドしてみると link 周りでコケることが分かったのでその原因についてまとめる。
前回との差分
前回の記事で gunit_large, server_unittest_library の2つがユニットテストをサポートする上で重要なライブラリであるという話を書いたが、それは間違いではなくそのまま。
問題は MYSQL_ADD_PLUGIN で指定する plugin_args にあった。ここに特定のキーワードが含まれる場合とそうでない場合で上記のライブラリにリンクされるかどうか結果が変わってくることが分かったというのが今回ここでする話である。
本題
前回の記事で紹介した手順にしたがってビルドをしていくと、MYSQL_ADD_PLUGIN の引数次第では gtest を含むユニットテストをビルドした場合に「undefined reference to」という見慣れたエラーが出てくる場合がある。
というわけでやや適当に書いてしまった前回記事から更に少し調べる必要に迫られたというわけである。
一度冷静になる
gunit_large の役割については前述の通りであるというので間違いないと思われるので、問題は servier_unittest_library をリンクするあたりにあるということがわかる。
というわけで今一度 server_unittest_library のビルドについて調べる。
MERGE_LIBRARIES_SHARED(server_unittest_library SKIP_INSTALL LINK_PUBLIC
sql_main
${MYSQLD_STATIC_PLUGIN_LIBS}
minchassis
ext::icu
# Import some core symbols. Other symbols needed by the unit test
# executables are pulled in transitively by symbol dependencies.
#
# Since everything has visibility("default") the library will
# export every symbol pulled in from the source libraries.
#
# If some symbols are still missing, they will be picked up from
# dependent libraries, since we LINK_PUBLIC.
# To see what symbols we need to import, remove LINK_PUBLIC above.
#
# The strings library uses visibility=hidden for all symbols,
# except those explicitly tagged with MYSQL_STRINGS_EXPORT.
# If we get ODR violations for executables using server_unittest_library,
# it means the symbol has been found in strings and
# server_unittest_library, which means the unit test is using
# some non-exported symbol from strings.
EXPORTS
builtin_perfschema_plugin # Pulls in the whole server.
mysql_service_mysql_rwlock_v1 # Pulls in minchassis
)
sql_main などは置いておいて、今ここで一番怪しそうなのは MYSQL_STATIC_PLUGIN_LIBS である。というかどうみてもそれぐらいしか可変であると思われるものはない。
頑張って実装を追う
ここで更に冷静になって、MYSQL_ADD_PLUGIN を読み直す。
... # Update mysqld dependencies SET (MYSQLD_STATIC_PLUGIN_LIBS ${MYSQLD_STATIC_PLUGIN_LIBS} ${target} ${ARG_LINK_LIBRARIES} CACHE INTERNAL "" FORCE) ...
どうやらここに到達させる必要があるというので間違いないと思われる。
というわけで、ここに MESSAGE をつけて cmake を実行してみることにする。
DEFAULT
まずは前回と同じ様に STORAGE_ENGINE DEFAULT な状態。
debug: ARCHIVE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib debug: BLACKHOLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib debug: CSV, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson debug: EXAMPLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib debug: FEDERATED, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson debug: HEAP, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson debug: INNOBASE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson debug: MYISAM, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library debug: MYISAMMRG, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson debug: NDBCLUSTER, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson debug: PERFSCHEMA, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib debug: TEMPTABLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson debug: NGRAM_PARSER, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson;ngram_parser debug: MYSQLX, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson;ngram_parser;mysqlx;ext::libevent;ext::icu;mysqlxmessages_lite;libprotobuf-lite;extra::rapidjson;ext::lz4;ext::zstd;ext::zlib
これを見るに server_unittest_library にリンクされるものが MYSQL_ADD_PLUGIN の該当箇所を通過するたびに追加されていくという理解で合っていることがわかる。
実際に DEFAULT がついている場合に通過する部分を見るに WITH_${plugin} = 1 にしているので実装とも合っている。
IF(ARG_DEFAULT) IF(NOT DEFINED WITH_${plugin} AND NOT DEFINED WITHOUT_${plugin} AND NOT DEFINED WITH_${plugin}_STORAGE_ENGINE) SET(WITH_${plugin} 1) ENDIF() ENDIF()
というわけで次にこの部分に到達するために必要な IF を見る。
# Build either static library or module IF (WITH_${plugin} AND NOT ARG_MODULE_ONLY)
WITH_${plugin} が true で MODULE_ONLY でない場合に到達するらしい。
MODULE_ONLY は引数で渡す場合にその shared library のみを作成してくれるもので、これを指定していると LINK_LIBRARIES の段階でエラーとなるので今回は関係ないといえば関係ないが、ユニットテストをサポートするときには必要ないだろう。
問題はその他である。WITH_${plugin} が true 相当にならないといけないので、その周辺を見ていく。
WITH_"${plugin}"_STORAGE_ENGINE
まずは -DWITH_EXAMPLE_STORAGE_ENGINE=1 にして DEFAULT を外した場合。
debug: ARCHIVE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib debug: BLACKHOLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib debug: CSV, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson debug: EXAMPLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib debug: FEDERATED, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson debug: HEAP, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson debug: INNOBASE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson debug: MYISAM, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library debug: MYISAMMRG, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson debug: NDBCLUSTER, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson debug: PERFSCHEMA, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib debug: TEMPTABLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson debug: NGRAM_PARSER, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson;ngram_parser debug: MYSQLX, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson;ngram_parser;mysqlx;ext::libevent;ext::icu;mysqlxmessages_lite;libprotobuf-lite;extra::rapidjson;ext::lz4;ext::zstd;ext::zlib
このパターンは MYSQL_ADD_PLUGIN の実装を見ても WITH_${plugin} = 1 を設定しているので、実装と合っている。
IF(WITH_${plugin}_STORAGE_ENGINE OR WITH_{$plugin} AND NOT WITHOUT_${plugin}_STORAGE_ENGINE AND NOT WITHOUT_${plugin} AND NOT ARG_MODULE_ONLY) SET(WITH_${plugin} 1)
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/cmake/plugin.cmake#L96-L102
MANDATORY
次に MANDATORY を指定した場合。これは必須ストレージエンジン or Plugin という意味合いで、見た範囲では InnoDB にこれがついている。
debug: ARCHIVE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib debug: BLACKHOLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib debug: CSV, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson debug: EXAMPLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib debug: FEDERATED, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson debug: HEAP, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson debug: INNOBASE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson debug: MYISAM, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library debug: MYISAMMRG, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson debug: NDBCLUSTER, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson debug: PERFSCHEMA, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib debug: TEMPTABLE, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson debug: NGRAM_PARSER, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson;ngram_parser debug: MYSQLX, MYSQLD_STATIC_PLUGIN_LIBS: archive;extra::rapidjson;ext::zlib;blackhole;extra::rapidjson;ext::zlib;csv;extra::rapidjson;example;ext::zlib;federated;extra::rapidjson;heap;heap_library;extra::rapidjson;innobase;sql_dd;sql_gis;ext::zlib;ext::lz4;extra::rapidjson;myisam;myisam_library;myisammrg;extra::rapidjson;ndbcluster;ndbclient_static;extra::rapidjson;perfschema;extra::rapidjson;ext::zlib;temptable;extra::rapidjson;ngram_parser;mysqlx;ext::libevent;ext::icu;mysqlxmessages_lite;libprotobuf-lite;extra::rapidjson;ext::lz4;ext::zstd;ext::zlib
これは実装を見ても WITH_${plugin} = 1 を設定しているので実装からしても合っている。
IF(ARG_MANDATORY) SET(WITH_${plugin} 1) SET(WITHOUT_${plugin} 0) ENDIF()
https://github.com/mysql/mysql-server/blob/mysql-8.0.33/cmake/plugin.cmake#L131C1-L134C10
おわりに
というわけで 3 パターンのビルド方法で unittest をサポートすることが出来ると分かったが、直前の記事でややミスってしまったので自信がない。
MySQL 探索記 ~自作プラグイン開発でユニットテストを気合いでサポートするための色々~
はじめに
どうも、どうにかこうにか MySQL の自作プラグイン開発で mysql-server 本体に手を加えずに gtest 等*1 を使ったユニットテストを実行したいと思い気がつけば 3 連休を溶かしていたけんつです。
MySQL のユニットテストは unittests/ 以下に実装が存在しており、各 Storage Engine やその他プラグインの実装ディレクトリ下には基本的にユニットテストは存在しない。*2 そのため、ユニットテストを書きたい場合は mysql-server 下の実装に手を加える必要がある。しかし、大抵の場合 git repository で自作プラグインを管理した時にどうにか mysql-server の実装にパッチを当てるなりしてビルドする必要が出てきてしまう。それはあまり嬉しいことではない。
というわけで、ここではどうにか mysql-server に手を加えずにユニットテストをサポートする方法をまとめる。
長々と書いたが、ここでやりたいことは unittest/ 以外で gtest を使ったテストを実装することである。
最初に書いておくが、ADD_EXECUTABLE, TARGET_LINK_LIBRARY で頑張る方法は大変苦行なのでおすすめしない。
前提
libmysqlclient-dev のみでは全然やりたいことなんか出来ねぇぜ*3 という大変ロックな人、または自作ストレージエンジンをやりたがる奇特な人向けとなっている。
つまり何かというと、mysql-server のソースコードを引っ張ってきて、自作プラグインのソースコードを配置し、MySQL ごとビルドする必要に迫られる上にそれをどうにか git repository で管理したい人向けである。
この記事ではみんな大好き EXAMPLE ストレージエンジンに少しだけ実装を追加し、その実装を gtest を使ってテストを書き、それを実行することを目的とする。
想定しているディレクトリ構成は以下の通り。
./storage/example/
|-- CMakeLists.txt
|-- ha_example.cc
|-- ha_example.h
|-- sample.cc
|-- sample.h
`-- tests
|-- CMakeLists.txt
`-- sample_test.cc
1 directory, 7 filesこの状態にした上で MySQL をビルドし tests ディレクトリ以下に存在するテストを実行する実行可能ファイルを吐き出させたいというところに目的がある。
気合で gtest を使えるようにする
テスト対象の実装を追加
以下の2つのファイルを storage/example 以下に追加する。
// sample.cc #include <mysql/psi/mysql_file.h> #include "sample.h" bool SampleUtil::returnTrue() { return true; } void SampleUtil::seek() { mysql_file_seek(0,0,0,0); }
// sample.h #ifndef EXAMPLE_SAMPLE_H #define EXAMPLE_SAMPLE_H class SampleUtil { public: static bool returnTrue(); static void seek(); }; #endif
EXAMPLE ストレージエンジンのビルド対象に追加する
上記のファイルを EXAMPLE ストレージエンジンのビルド対象に含める。
diff --git a/storage/example/CMakeLists.txt b/storage/example/CMakeLists.txt index 99e79270399..5f368c667bf 100644 --- a/storage/example/CMakeLists.txt +++ b/storage/example/CMakeLists.txt @@ -24,7 +24,7 @@ DISABLE_MISSING_PROFILE_WARNING() ADD_DEFINITIONS(-DMYSQL_SERVER) IF(WITH_EXAMPLE_STORAGE_ENGINE AND NOT WITHOUT_EXAMPLE_STORAGE_ENGINE) - MYSQL_ADD_PLUGIN(example ha_example.cc + MYSQL_ADD_PLUGIN(example ha_example.cc sample.cc STORAGE_ENGINE DEFAULT LINK_LIBRARIES ext::zlib @@ -36,3 +36,6 @@ ELSEIF(NOT WITHOUT_EXAMPLE_STORAGE_ENGINE) LINK_LIBRARIES ext::zlib ) ENDIF() + +ADD_SUBDIRECTORY(tests/)
テストファイルを追加する
tests ディレクトリを掘ってからテストファイルと CMakeLists.txt を追加する。
// tests/sample_test.cc #include <gtest/gtest.h> #include "sample.h" TEST(sample_returnTrue, success) { bool res = SampleUtil::returnTrue(); ASSERT_EQ(res, true); } TEST(sample_seek, success) { SampleUtil::seek(); }
# tests/CMakeLists.txt INCLUDE_DIRECTORIES( ${CMAKE_SOURCE_DIR}/storage/example ) SET(TESTS sample_test.cc ) SET(ALL_EXAMPLE_TESTS) FOREACH (test ${TESTS}) LIST(APPEND ALL_EXAMPLE_TESTS ${test}) ENDFOREACH () MYSQL_ADD_EXECUTABLE(example_tests ${ALL_EXAMPLE_TESTS} ENABLE_EXPORTS ADD_TEST example_tests LINK_LIBRARIES gunit_large server_unittest_library )
ビルドする
今回は EXAMPLE ストレージエンジンもビルドしたいので以下のようにビルドする。
$ mkdir build && cd $_ $ cmake ../ -DCMAKE_BUILD_TYPE=Debug -DWITH_BOOST=./boost -DDOWNLOAD_BOOST=1 -DWITH_EXAMPLE_STORAGE_ENGINE=1 $ make -j12
テストを実行する
$ cd build/runtime_output_directory $ ./example_tests [==========] Running 2 tests from 2 test suites. [----------] Global test environment set-up. [----------] 1 test from sample_returnTrue [ RUN ] sample_returnTrue.success [ OK ] sample_returnTrue.success (0 ms) [----------] 1 test from sample_returnTrue (0 ms total) [----------] 1 test from sample_seek [ RUN ] sample_seek.success [ OK ] sample_seek.success (0 ms) [----------] 1 test from sample_seek (0 ms total) [----------] Global test environment tear-down [==========] 2 tests from 2 test suites ran. (0 ms total) [ PASSED ] 2 tests.
ヨシ!
ここまでに何が行われたのか
この様に書いてみれば大変楽な作業に思えるが、ここに至るまでに 3 日程費やしただけあり、どうやってここまでたどり着いたかが割と重要だった。
既存実装の調査と紆余曲折
storage/perfschema の unittest
storage/**/ 下に unittest が存在する場合というのがまず一番嬉しい(簡単であろう)ケースである。なので、まずはそこから調査する。ここでは perfschema が unittest を利用していたのでそこから。
そして恐らく重要なのはこのあたりである。これは unittest ディレクトリ以下のテストケースに対して MYSQL_ADD_EXECUTABLE*4 を実行し、テストファイルごとに必要なライブラリをリンクし、実行可能ファイルを生成してくれる。
# storage/perfschema/unittest/CMakeLists.txt ... MACRO (PFS_ADD_TEST name) MYSQL_ADD_EXECUTABLE(${name}-t ${name}-t.cc ADD_TEST ${name}) TARGET_LINK_LIBRARIES(${name}-t mytap perfschema mysys pfs_server_stubs strings ext::icu) ENDMACRO() SET(tests pfs_instr_class pfs_instr_class-oom pfs_instr pfs_instr-oom pfs_account-oom pfs_host-oom pfs_user-oom pfs_noop pfs pfs_misc pfs_mem ) FOREACH(testname ${tests}) PFS_ADD_TEST(${testname}) ENDFOREACH() ...
mysql-server/storage/perfschema/unittest/CMakeLists.txt at trunk · mysql/mysql-server · GitHub
ここにあるテストコードは mytap*5 を利用したものだが、これの boost test library 版や gtest 版を実装してみたところ、pfs や dd 等のテスト実行時に呼ばれる依存関係を解決できずにビルドに失敗してしまった。*6
また TARGET_LINK_LIBRARIES に必要となるライブラリをひたすら指定するという、これは mysql-server の実装を隅から隅まで知らないといけないのレベルで面倒だったので断念。
脳筋戦法
ここで心が折れそうになり、だったら ha_example をテストの実行可能ファイルにそのままリンクしてやればいいのではという脳筋戦法にたどり着いた。しかし、その場合も perfschema と同様の問題にぶち当たる上に MYSQL_ADD_PLUGIN に指定されるビルドタイプの影響をモロに受ける*7 という別問題が出てきたので早々に断念した。
InnoDB の unittest
やはり InnoDB である。やはり InnoDB、お前は最高である。
というわけで gtest を利用しているコードを検索しまくっていると unittest/gunit/innodb/ 以下にごっそり存在していることが分かったので、それを参考にする。
# unittet/gunit/innodb/CMakeLists.txt ... INCLUDE_DIRECTORIES( ${CMAKE_SOURCE_DIR}/sql ${CMAKE_SOURCE_DIR}/storage/innobase/include ) ... SET(TESTS #example fil_path ha_innodb log0log mem0mem os0file os0thread-create srv0conc sync0rw ut0crc32 ut0lock_free_hash ut0math ut0mem ut0new ut0rnd ) ... SET(ALL_INNODB_TESTS) FOREACH(test ${TESTS}) LIST(APPEND ALL_INNODB_TESTS ${test}-t.cc) ENDFOREACH() ... MYSQL_ADD_EXECUTABLE(merge_innodb_tests-t ${ALL_INNODB_TESTS} ENABLE_EXPORTS ADD_TEST merge_innodb_tests-t LINK_LIBRARIES gunit_large server_unittest_library ) ...
https://github.com/mysql/mysql-server/blob/trunk/unittest/gunit/innodb/CMakeLists.txt
やっていることの本質としてはこの前に出てきた perfschema と同じではある。ストレージエンジンの実装に存在する必要な header ファイルの場所と、テストで利用しているであろう boost, gmock の header を教えてやってから、複数のテストをまとめた実行可能ファイルを生成している。そしてここで一番大きいのは MYSQL_ADD_EXECUTABLE に出てくる gunit_large, server_unittest_library の存在が大変それっぽい。
ここで最初に紹介した方法に戻り、実装を少し修正してからビルドすると gunit_large, server_unittest_library をリンクし直していることがわかる。
$ make -j12 ... [ 96%] Linking CXX shared library library_output_directory/libserver_unittest_library.so [ 96%] Linking CXX executable ../runtime_output_directory/mysqld [ 96%] Built target server_unittest_library Consolidate compiler generated dependencies of target example_tests [ 96%] Linking CXX executable ../../../runtime_output_directory/avid_tests [ 96%] Linking CXX executable ../../../runtime_output_directory/pfs_connect_attr-t [ 96%] Linking CXX executable ../../../runtime_output_directory/group_replication_member_version-t [ 96%] Linking CXX executable ../../../../plugin_output_directory/minimal_chassis_test_driver-t [ 96%] Linking CXX executable ../../../runtime_output_directory/group_replication_member_info-t [ 96%] Linking CXX executable ../../../../plugin_output_directory/reference_cache-t [ 96%] Linking CXX executable ../../../runtime_output_directory/group_replication_compatibility_module-t [ 96%] Linking CXX executable ../../../runtime_output_directory/example_tests [ 96%] Linking CXX executable ../../../runtime_output_directory/merge_keyring_file_tests-t [ 96%] Linking CXX executable ../../../runtime_output_directory/merge_innodb_tests-t [ 96%] Linking CXX executable ../../runtime_output_directory/merge_large_tests-t [ 96%] Built target mysqld [ 96%] Linking CXX executable ../../../runtime_output_directory/group_replication_mysql_version_gcs_protocol_map-t [ 96%] Built target minimal_chassis_test_driver-t [ 96%] Linking CXX executable ../../../runtime_output_directory/group_replication_gcs_mysql_network_provider-t [ 96%] Built target reference_cache-t [ 96%] Built target avid_tests [ 96%] Linking CXX executable ../../../runtime_output_directory/merge_temptable_tests-t ...
というわけで unittest/gunit/CMakeLists.txt を見てみる。
# unittest/gunit/CMakeLists.txt ... # gunit_large ADD_STATIC_LIBRARY(gunit_large benchmark.cc gunit_test_main_server.cc test_utils.cc thread_utils.cc LINK_LIBRARIES ext::icu ext::zlib ) ...
https://github.com/mysql/mysql-server/blob/trunk/unittest/gunit/CMakeLists.txt
gunit_large に関しては明らかにそれらしい実装たちを link して static library として吐いてくれる。むしろこれが無いと mysql-server の絡む gtest が実行できない*8 のではというところまである。
mysql-server/unittest/gunit/gunit_test_main_server.cc at trunk · mysql/mysql-server · GitHub
次に server_unittest_library について。こいつは project root 直下の CMakeLists.txt に記述が存在する。
# ./CMakeLists.txt ... MERGE_LIBRARIES_SHARED(server_unittest_library SKIP_INSTALL LINK_PUBLIC sql_main ${MYSQLD_STATIC_PLUGIN_LIBS} minchassis ext::icu ... ADD_LIBRARY(server_unittest_library STATIC ${DUMMY_SOURCE_FILE}) TARGET_LINK_LIBRARIES(server_unittest_library perfschema) TARGET_LINK_LIBRARIES(server_unittest_library sql_main) TARGET_LINK_LIBRARIES(server_unittest_library minchassis) TARGET_LINK_LIBRARIES(server_unittest_library ext::icu) ...
https://github.com/mysql/mysql-server/blob/trunk/CMakeLists.txt
ここでは実装を見るにビルドオプションによって必要なライブラリをリンクするか、ダミーファイルを持つ static library を生成してくれそう。*9
おわりに
というわけで、3 日間に渡り格闘した気の狂ったプラグイン自作におけるユニットテストのサポートは完了した。*10
これで少しだけ mysql-server のユニットテストについて詳しくなれたと思うが、ちゃんとテストコードを実装してみて「こうは言ったものの、やっぱりだめだった」となったら気合でどうにかする。
*1:gtest 以外にも Boost Test Library や mytap なるものを使ったテストも行けそうではあるが試してはいない。恐らく gtest > mytap > Boost Test Library の順番で簡単にサポートできる。
*2: 一部、perfschema などはその通りではない
*3: 例: InnoDB のバッファープールのポインタを直接参照する等
*4:実行可能ファイルを吐いてくれる MySQL 独自の便利な cmake マクロ
*5:MySQL: Unit Testing Using TAP
*6:この記事の先頭で mysql_file_seek などが含まれているのはこのケースに当てはまる場合があるため。それらを利用しない実装であれば呼び出しても undefined references で死ぬことはなかった。
*7:EXAMPLE Storage Engine の CMakeLists.txt で言うところの DEFAULT のこと。これが MODULE_ONLY だとそもそもリンク出来ない等の仕様が存在することが分かったが、その観点で戦い始めた話はまた別の機会に。
*8:正確にはできないことも無いが途方もない労力がかかる
*9:こいつ自体がリンクされていないとどうなるかは分かったが何故そうなったかはわかっていない。sql_main が含まれていることから server_unittest_library が無いと恐らく server layer に依存した処理がビルドで死ぬと思われる。
*10:サポートしたは良いものの、まだテストコード自体はちゃんと書いていないのでもしかしたらだめかもしれない
MySQL ハンドラーレイヤー探索記 ~無限 Empty Set 編~
はじめに
どうも InnoDB に詳しくなろうと思って色々調べていたら何故か mysql-server レイヤーに詳しくなっていっているけんつです。
最近 InnoDB と最もシンプルな実装であろう tina を見比べつつ、適当に実装を変えて遊んでいたら無限 Empty Set に悩まされたのでその挙動について書く。
ハンドラーの挙動
SELECT が開始されると以下の順番で handler のメソッドを呼び出す。
- handler::store_lock
- handler::external_lock
- hander::info
- handler::rnd_init
- handler::extra
- handler::rnd_next ×レコード数
- handler::rnd_next ←これがめちゃくちゃ大事だった
- handler::extra
- handler::external_lock
- handler::extra
rnd_next メソッドがレコード数分呼ばれて、都度引数として受け取った uchar * のバッファーにデータを詰めて結果が返ってくるという風になっている。
ここでみんな大好き example ストレージエンジンを見てみると、以下のような実装が存在する。
int ha_example::rnd_next(uchar *) {
int rc;
DBUG_TRACE;
rc = HA_ERR_END_OF_FILE;
return rc;
}https://github.com/mysql/mysql-server/blob/trunk/storage/example/ha_example.cc#L454-L459
HA_ERR_END_OF_FILE が返された時点でサーバーレイヤーは rnd_next を繰り返し呼び出すことをやめるようになっている。
最低限必要なのは適切なタイミングで HA_ERR_END_OF_FILE を返しスキャンを行うことを停止させることと、バッファに適切なデータを詰めるということ。
波乱の幕開け
SELECT 以前にいつも不思議だった write_row の引数にある uchar * の値は一体何が詰まってくるのか、rnd_next のバッファには何を詰めれば良いのかということを調べていた。
色々調べていると write_row はインサートされた行を以下のドキュメントに記載のフォーマットで詰めてくるということが分かった。
MySQL: Row format
ここで一行 INSERT してバッファを保持しつつ SELECT 時に全く同じバッファを詰めて返せるのかということを検証していたがこれが完全に波乱の幕開けであった。
tina を改造するのは面倒だったので example ストレージの rnd_next をいじって次のようにしてみた。
int ha_example::rnd_next(uchar *buf) {
int rc;
DBUG_TRACE;
memcpy(buf, insertBuf, 1024);
rc = HA_ERR_END_OF_FILE;
return rc;
}これで SELECT * FROM をやれば、追加した行と同じ行が返ってくるはずだと思っていたが返ってきたのは Empty Set であった。
この検証に数時間費やし、tina と同様の実装を改造して一行だけ返すようにしても何故かだめだった。
なので、ここから地獄のデバッグ作業の幕開けとなる。
なんで Empty Set なのか
一つずつ順にコードパスを遡っていき、怪しそうな場所を見つけた。
どうやらここがハンドラーの rnd_next を呼び出して、結果をみつつごにょごにょやっているところらしい。
https://github.com/mysql/mysql-server/blob/trunk/sql/iterators/basic_row_iterators.cc#L219
実装を見るに HA_ERR_RECORD_DELETED を返してスレッドが閉じていない場合はスキップするという処理らしい。
で、その TableScanIterator の Read メソッドはこの部分が呼び出している。
https://github.com/mysql/mysql-server/blob/trunk/sql/sql_union.cc#L1770
その後は以下の処理に入り break となる。
https://github.com/mysql/mysql-server/blob/trunk/sql/sql_union.cc#L1775-L1776
ここまで分かったところでそのすぐ下に send_record_ptr と thd->current_found_rows なるめちゃくちゃ怪しそうな変数の存在が重要になってくる。というかどう見てもここである。
更に詳細なことは調べていないがこれが何かというと、break に入った段階で send_record_ptr は更新されない上に明らかにそれっぽい send_data も呼ばれないのでバッファに何を詰めても恐らく無視している。
というわけで一回 rnd_next が呼び出された状態では 0 を返し、もう一度 rnd_next が呼ばれた時に HA_ERR_END_OF_FILE を返してやると無事に一行結果が返ってきた。
つまり rnd_next はレコード数分 + HA_ERR_END_OF_FILE を返す分が必要になるのでレコード数 + 1 回呼ばれるのが正常らしい。
余談
write_row のバッファをそのまま使って rnd_next のバッファに詰めてやると insert した結果をそのまま表示できたので rnd_next のバッファも Row Format に従ったバイナリ形式であれば mysql-server が解釈してくれるというので間違いないらしい。なんなら Row Format のドキュメントにも書いていた。
おわりに
本当は InnoDB の諸々の実装と最もシンプルなストレージエンジンを見比べるつもりだったが思わぬところで Server レイヤーの仕組みに少し詳しくなった。
UDF と char * と時々 --binary-as-hex
はじめに
最近 UUID に頭を悩ませまくった結果、ULID なるいいものがあると知ったので気分転換がてら MySQL の UDF (今で言うところの Loadable Function) を実装している。UDF を書くこと自体が初めてだったので、引っかかったところを後の自分のために残す。
mysql-ulid-plugin
github.com
今作りかけているものがこれ。実際に動かしてみた感じでは、Timestamp の変換は恐らく上手くいっているが乱数部分が全然変わっていない雰囲気を感じるので後でどうにかする。
UDF をインストールする
ビルドした前提で話す。
- plugin dir 以下に ulid.so を配置する
- CREATE FUNCTION ulid RETURNS STRING SONAME 'ulid.so' で関数を適用する
- SELECT ULID() でそれっぽい値が返っているならば成功
mysql> CREATE FUNCTION ulid RETURNS STRING SONAME 'ulid.so'; mysql> SELECT ULID(); +----------------------------+ | ulid() | +----------------------------+ | 0001JANH8A6Q86QD0000000000 | +----------------------------+ 1 row in set (0.00 sec)
やっぱりどう見ても randomness なところが固定値っぽくなっている。まじで怪しい。
ハマりどころ
初期化関数の戻り値問題
_init 関数に UDF の初期化処理を記述していくことになるが、ここでややハマった。
特に今回は UDF 全体で使いたい情報が今のところはないので、実装は空になっているがこんな感じに書いている。
extern "C" bool ulid_init(UDF_INIT *, UDF_ARGS *, char *) { return false; }
問題はこの return false; である。初期化処理に成功したら true を返せば良いと脳死で考えていたらこんな自体にぶち当たった。
mysql> CREATE FUNCTION ulid RETURNS STRING SONAME 'ulid.so'; Query OK, 0 rows affected (0.01 sec) mysql> SELECT ULID(); ERROR 1123 (HY000): Can't initialize function 'ulid';
初期化できないとな…。そう、ここは初期化に成功したら false を返すべきだったのである。まさに予想外。
ちゃんと sql/udf_example.cc とかを見ておけば良かったかもしれない。
char * で返した値が何故か hex で表示される
mysql> CREATE FUNCTION ulid RETURNS STRING SONAME 'ulid.so'; Query OK, 0 rows affected (0.01 sec) mysql> select ulid(); +--------------------------------------------------------+ | ulid() | +--------------------------------------------------------+ | 0x303030314A414E48375850344D57574652303030303030303030 | +--------------------------------------------------------+ 1 row in set (0.01 sec)
次にぶつかったのがこの問題である。 char *result に値を突っ込んで返しているのだから、Base32 の文字列が表示されるはずだったが、何故か 16 進数表記になっている。
この件は bugs.mysql.com に答えがあった。
I confirm that invoking the client with "--binary-as-hex=0" fixes things. I had missed this (for me) crucial change! I should have read
MySQL Bugs: #99480: char* UDF returning hexadecimal string rather than string
mysql-client を使う時に binary-as-hex=0 を入れろよ、とな。
実際にそれでやると上手くいった。
$ ./bin/mysql -uroot -proot --binary-as-hex=0 mysql: [Warning] Using a password on the command line interface can be insecure. Welcome to the MySQL monitor. Commands end with ; or \g. Your MySQL connection id is 9 Server version: 8.0.33-debug Source distribution Copyright (c) 2000, 2023, Oracle and/or its affiliates. Oracle is a registered trademark of Oracle Corporation and/or its affiliates. Other names may be trademarks of their respective owners. Type 'help;' or '\h' for help. Type '\c' to clear the current input statement. mysql> select ulid(); +----------------------------+ | ulid() | +----------------------------+ | 0001JANH8A6Q86QD0000000000 | +----------------------------+ 1 row in set (0.00 sec)
ただ、やはり char * が 16 進数表示されるということには初見で元気に躓きそうな気がする。
おわりに
ここだけ抑えておけば文字列を返す UDF はいつでもどうにかできそうな気がしている。
UDF は一段落しそうだが、ULID を構築するための乱数が難しい。乱数ってなんでこんなに難しいんだ。
読むと幸せになれる
公式のドキュメントがある程度充実していて助かった。